1206. Design Skiplist

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Design a Skiplist without using any built-in libraries.

A skiplist is a data structure that takes O(log(n)) time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.

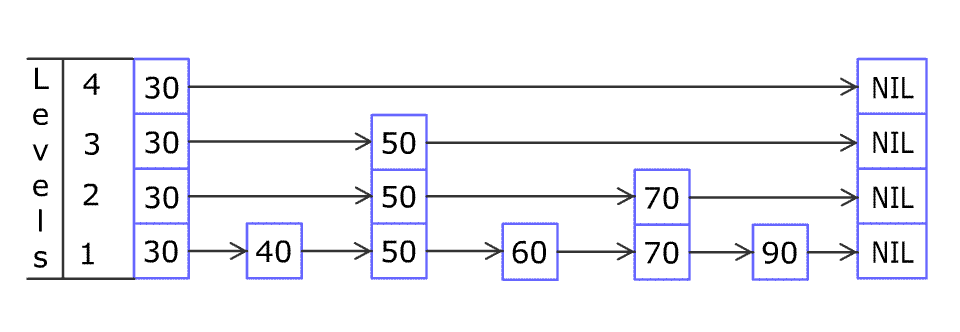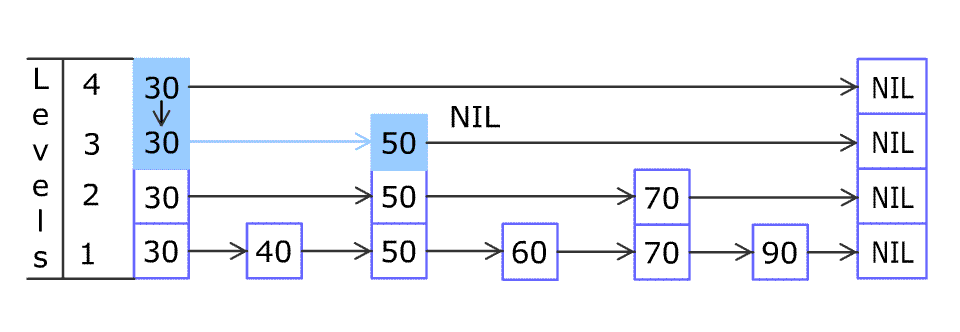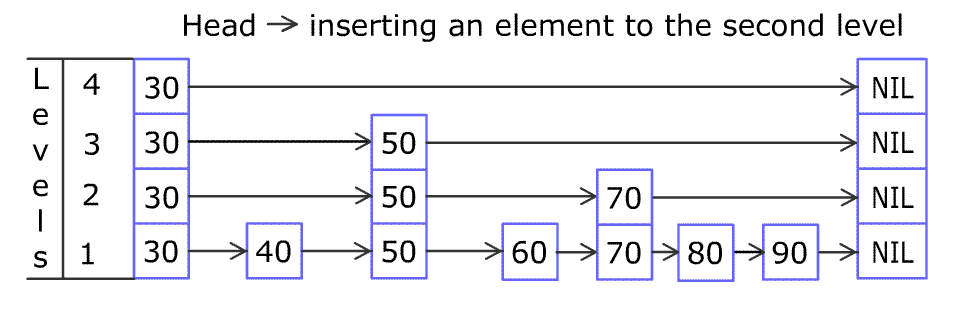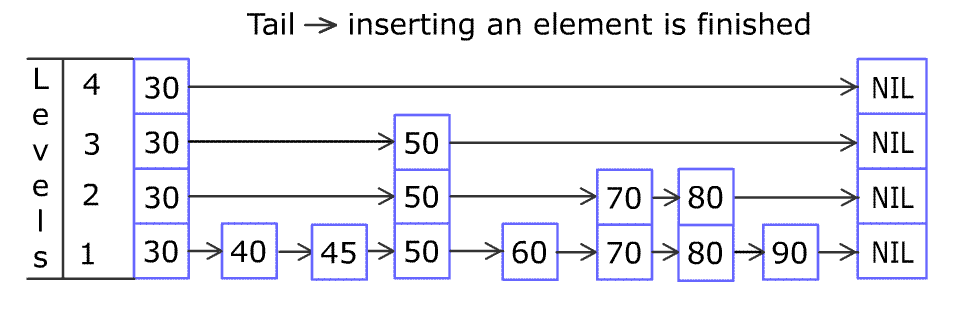
For example, we have a Skiplist containing [30,40,50,60,70,90] and we want to add 80 and 45 into it. The Skiplist works this way:

Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than O(n). It can be proven that the average time complexity for each operation is O(log(n)) and space complexity is O(n).

See more about Skiplist: https://en.wikipedia.org/wiki/Skip_list

Implement the Skiplist class:

• Skiplist() Initializes the object of the skiplist.
• bool search(int target) Returns true if the integer target exists in the Skiplist or false otherwise.
• void add(int num) Inserts the value num into the SkipList.
• bool erase(int num) Removes the value num from the Skiplist and returns true. If num does not exist in the Skiplist, do nothing and return false. If there exist multiple num values, removing any one of them is fine.

Note that duplicates may exist in the Skiplist, your code needs to handle this situation.

Example 1:

Input
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
Output
[null, null, null, null, false, null, true, false, true, false]

Explanation
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0);  // return False, 0 is not in skiplist.
skiplist.erase(1);  // return True
skiplist.search(1); // return False, 1 has already been erased.

Constraints:

• 0 <= num, target <= 2 * 104
• At most 5 * 104 calls will be made to search, add, and erase.

Code

class Skiplist {
    class Node {
        int val;
        Node next, down;

        public Node(int val, Node next, Node down) {
            this.val = val;
            this.next = next;
            this.down = down;
        }
    }

    Node head;
    Random rand;

    public Skiplist() {
        head = new Node(-1, null, null);
        rand = new Random();
    }

    public void add(int num) {
        Stack<Node> stack = new Stack<>();
        Node cur = head;

        // 需要从最底层插入node 所以使用stack
        // 之后从最底层开始插入
        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }
            stack.push(cur);
            cur = cur.down;
        }

        boolean insert = true;
        Node down = null;

        // 每次只有50%的概率插入到上一层
        while (insert && !stack.isEmpty()) {
            cur = stack.pop();
            // 每次创建新node 并指向下一层的这个node
            Node one = new Node(num, cur.next, down);
            cur.next = one;
            down = one;

            insert = rand.nextDouble() < 0.5;
        }

        if (insert)
            head = new Node(-1, null, head);
    }

    public boolean search(int target) {
        Node cur = head;

        while (cur != null) {
            while (cur.next != null && cur.next.val < target) {
                cur = cur.next;
            }

            if (cur.next != null && cur.next.val == target)
                return true;

            cur = cur.down;
        }

        return false;
    }

    public boolean erase(int num) {
        Node cur = head;
        boolean found = false;

        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }

            if (cur.next != null && cur.next.val == num) {
                found = true;
                cur.next = cur.next.next;
            }

            cur = cur.down;
        }

        return found;
    }
}