2458. Height of Binary Tree After Subtree Removal Queries

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the $i^{th}$ query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

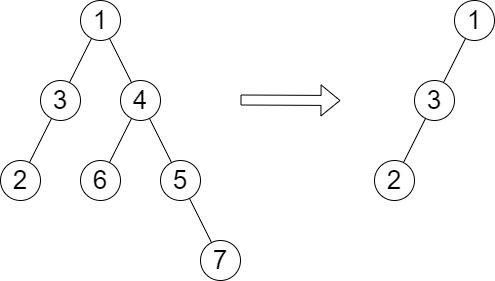
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:

- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

• The number of nodes in the tree is n.
• $2 <= n <= 10^5$
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• $1 <= m <= min(n, 10^4)$
• 1 <= queries[i] <= n
• queries[i] != root.val

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    class Node {
        int val, height;

        public Node(int val, int height) {
            this.val = val;
            this.height = height;
        }

        public String toString() {
            return String.format("[%d,%d]", val, height);
        }
    }

    Map<Integer,Integer> dep;
    Map<Integer,Integer> hei;
    Map<Integer,Queue<Node>> map;

    public int[] treeQueries(TreeNode root, int[] queries) {
        dep = new HashMap<>();
        hei = new HashMap<>();
        map = new HashMap<>();

        dfs(root, 0);

        for(int val : dep.keySet()){
            int depth = dep.get(val);
            int height = hei.get(val);
            if(!map.containsKey(depth)) {
                Queue<Node> queue = new PriorityQueue<Node>((a, b) -> b.height - a.height);
                map.put(depth, queue);
            }
            Queue<Node> queue = map.get(depth);
            queue.add(new Node(val, height));
            map.put(depth, queue);
        }

        int[]res = new int[queries.length];

        for(int i = 0; i < queries.length; i++) {
            int val = queries[i];
            int depth = dep.get(val);

            Queue<Node> cous = map.get(depth);
            if(cous.size() == 1) {
                res[i] = depth - 1;
            } else {
                Node first = cous.remove();
                if(first.val == val){
                    Node second = cous.remove();
                    res[i] = depth + second.height;
                    cous.add(first);
                    cous.add(second);
                } else {
                    res[i] = depth + first.height;
                    cous.add(first);
                }
            }
        }

        return res;
    }

    private int dfs(TreeNode root, int depth){
        if(root == null) return -1;

        dep.put(root.val, depth);
        int maxHeight = Math.max(dfs(root.left, depth + 1), dfs(root.right, depth + 1)) + 1;
        hei.put(root.val, maxHeight);

        return maxHeight;
    }
}