JIAKAOBO

LeetCode

venmo
wechat

感谢赞助!

  • ㊗️
  • 大家
  • offer
  • 多多！

Problem

You are given an array of points on the X-Y plane points where points[i] = [xi, yi]. The points form a polygon when joined sequentially.

Return true if this polygon is convex and false otherwise.

You may assume the polygon formed by given points is always a simple polygon. In other words, we ensure that exactly two edges intersect at each vertex and that edges otherwise don’t intersect each other.

Example 1:

img

Input: points = [[0,0],[0,5],[5,5],[5,0]]
Output: true

Example 2:

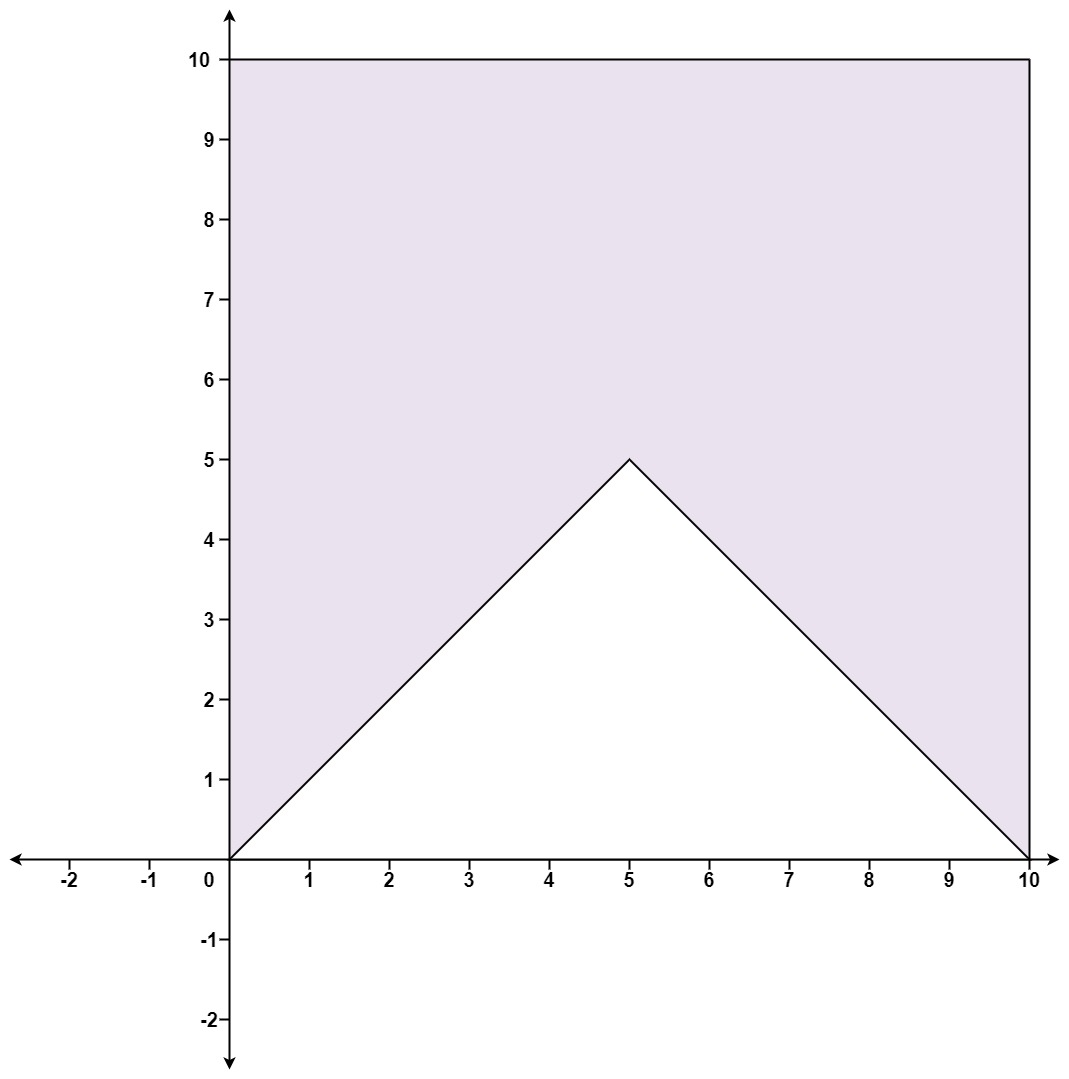
Input: points = [[0,0],[0,10],[10,10],[10,0],[5,5]]
Output: false

Constraints:

  • 3 <= points.length <= 10^4
  • points[i].length == 2
  • -10^4 <= x_i, y_i <= 10^4
  • All the given points are unique.

Code

Convex Polygon 凸多边形

参考blog

向量的叉乘，即求同时垂直两个向量的向量，即c垂直于a，同时c垂直于b

c = a×b = (ay * bz - by * az, bx * az - ax * bz , ax * by - bx * ay)

以上图为例a(1,0,0),b(0,1,0),c = a × b = (0,0,1)

叉乘的几何意义

  • |c|=|a×b|=|a||b|sinα (α为a，b向量之间的夹角）
  • |c| = a,b向量构成的平行四边形的面积 （如下图所示的平行四边形）

叉乘的拓展

在一般的常识或者教科书中规定叉乘只有3d才拥有，其实2d也可以拓展出来一个叉乘形式，而且非常有用。

拓展方式：假设有两个2d向量a,b，我们直接把他们视为3d向量，z轴补0，那么这个时候的a，b向量的叉乘结果c, cx = 0, cy = 0, cz = axby - bxay,

这个时候可以把2d的叉乘值定义一个值，而不是一个向量，那么这个值 k = cz = ax * by - bx * ay，我们可以通过这个k值得到很多有用的性质

  • a, b向量构成的平行四边形的面积
  • 如果k > 0时, 那么a正旋转到b的角度为 < 180°, 如果k<0, 那么a正旋转到b的角度为>180°, 如果k=0 那么a, b向量平行
class Solution {
    public boolean isConvex(List<List<Integer>> points) {
        int flag = 0;
        
        int size = points.size();
        
        for (int i = 0; i < size; i++) {
            List<Integer> a = points.get(i);
            List<Integer> b = points.get((i + 1) % size);
            List<Integer> c = points.get((i + 2) % size);
            
            int orientation = helper(a.get(0), a.get(1), b.get(0), b.get(1), c.get(0), c.get(1));
            
            if (orientation == 0) {
                continue;
            }
            
            if (flag == 0) {
                flag = orientation;
            } else if (flag != orientation) {
                return false;
            }
        }
        
        return true;
    }

    public int helper(int ax, int ay, int bx, int by, int cx, int cy) {
        int val = (ax - bx) * (cy - by) - (cx - bx) * (ay - by);
        
        if(val == 0) return 0;
        
        return val > 0 ? 1 : -1;
    }
}